Reproducing a paper on task-based learning for electric grid scheduling
Link to original paper: https://arxiv.org/abs/1703.04529
Link to Github repository for reproducing the paper: https://github.com/mianakajima/e2e-model-learning
Motivation
I was interested in how machine learning could be used to help fight climate change and came across a paper “Tackling Climate Change with Machine Learning” by Rolnick et al (which I will refer to as the metastudy). At my previous job, I worked a lot with electrification of buildings. There was always discussion about the future implications on the grid of electrifying, especially as the grid shifted to more renewable and variable sources of energy.
One of the items discussed in the metastudy was how machine learning could be used to aid the grid shift to more renewable sources. For example, machine learning could be used to better forecast supply and demand on the grid, which would be necessary since renewable resources (like the sun and wind) would make energy supply more variable and harder to predict. The paper I reproduced was one of the papers mentioned as an example of work in this area. The metastudy mentioned that this paper produced electricity demand forecasts trying to optimize for electricity scheduling costs and the same concept could be used to produce forecasts that would reduce greenhouse gas emissions (GHG). Optimizing for both electricity scheduling costs and reducing GHG emissions seemed really relevant and important so I immediately wanted to try it out!
Concepts
The purpose of the paper was to propose a machine learning method that may be useful for optimization problems. For example, for electric grid scheduling, we may want to minimize the grid cost. To do that, traditionally, one may try to forecast the demand as accurately as possible and schedule to meet the predicted demand. In an ideal world, your prediction would exactly meet the demand and your grid cost would be minimized.
Since we don’t live in an ideal world though, the model will probably still have errors! This paper proposes fine-tuning the prediction model according to the task loss, or the cost associated with what you are trying to optimize (in this case, the grid cost).
In the diagram below, I drew out how the process works.
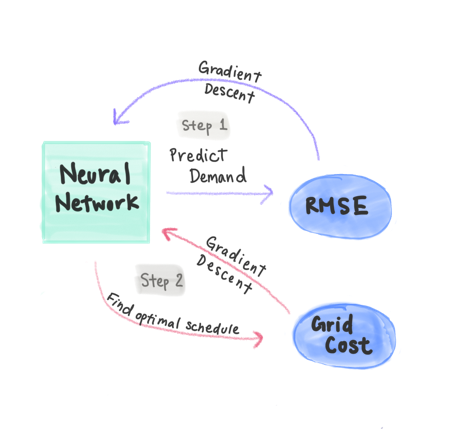
- Step 1: Train our initial model.
- We first train a model (a neural network in this case) to predict the electricity demands using a traditional root mean square error (RMSE) loss function. We train this model over many epochs.
- Step 2: Fine-tune our model.
- We then use the neural network to give a probablistic prediction of what the demand would be. We can use these predictions to find the optimal electric generation schedule given some costs for undergenerating or overgenerating.
- Actually solving this optimization function involves a lot of math and I write a bit more about it here.
- After figuring out the optimal schedule, we can calculate what is the actual grid cost. We now use this grid cost to perform gradient descent on the model weights, rather than the RMSE loss function, over many epochs.
- We then use the neural network to give a probablistic prediction of what the demand would be. We can use these predictions to find the optimal electric generation schedule given some costs for undergenerating or overgenerating.
Problem
The problem we want to solve is to create the next day’s electric generation schedule. This consists of one electricity generation scheduled per hour, so a total of 24 hours.
For the initial model, we use a feedforward neural net with features such as the past load, past and future temperature and indicators of the day of week/holidays/daylight savings time. Each layer also implemented batch normalization and drop out regularization.
The optimization problem we would like to solve is to minimize the grid cost. We assume that there are costs for overgenerating and undergenerating, and the cost of undergenerating is much higher than overgenerating.
The paper assumes the optimization problem looks like this:
\[\min_{z \in \mathbb{R}^{24}} \sum_{i = 1}^{24} \mathbb{E}_{y~p(y\vert x;\theta)} [\gamma_s[y_i -z_i]_+ + \gamma_e[z_i - y_i]_+ + \frac{1}{2}(z_i - y_i)^2]\] \[s.t. \vert z_i - z_{i - 1} \vert \leq c_r \forall i\]Where:
- $z_i$ : Electricity generation scheduled for every hour $i$
- $y_i$ : Demand, which we assume comes from a Gaussian distribution
- $\gamma_s$: The cost of undergenerating
- $\gamma_e$: The cost of overgenerating
- $c_r$: Ramping constant (we assume the energy generation cannot change excessively from one hour to the next)
- $[x]_+$ : Function meaning take the maximum of $x$ or 0.
The $\gamma_s$ and $\gamma_e$ values we use are 50 and 0.5 respectively.
The data used was 4 years of electricity load data from PJM (2008 through 2011). The last year was used as a test set.
Results
Below we compare the initial neural net trained on the RMSE loss function (RMSE loss model) with the final model that has been fine-tuned with the task loss (Task loss model). The graphs show the average RMSE, accuracy and task loss for each hour in test dataset.
The RMSE loss model had a lower RMSE than the task loss model by about 33%. On the other hand, the Task loss model did much better on reducing task loss than the RMSE loss model and showed an improvement of about 30 times!
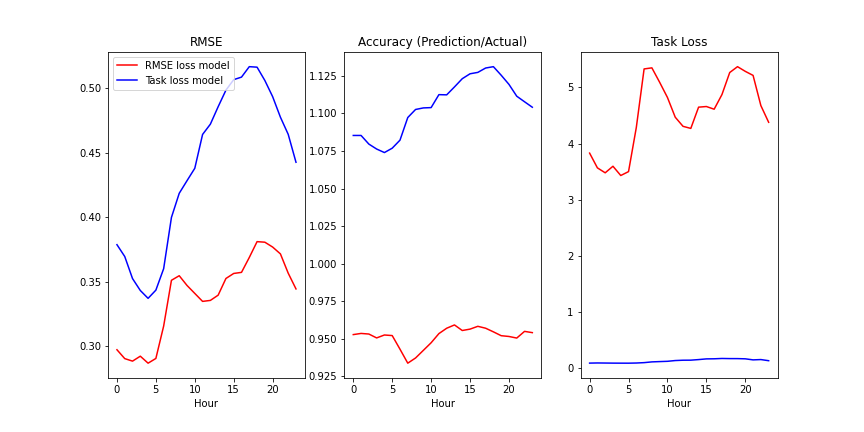
This scenario ended up being exactly the case where task-based learning would be helpful. In training, the accuracy of the model was pretty good - 99.7% on average. However on the test dataset, the accuracy dropped to 95.1% which led to almost doubling the task loss in the test scenario.
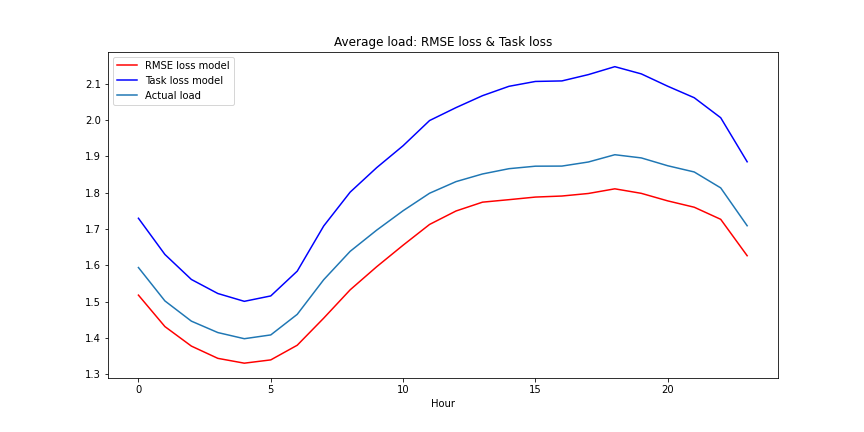
On the other hand, in order to compensate for the high cost of underproducing, the Task loss model seems to have learned to overschedule generation compared to the actual load. Although the accuracy is much lower (overpredicting by ~10%), the Task loss model is able to meet the end goal of operating the grid with lower costs better.
The graph below shows the average learned electric schedule over a year compared to the actual load in the test dataset.
Experimentation with Differing Weights
Now the fun part! After implementing the model from the paper, I decided to try playing around with different optimization scenarios.
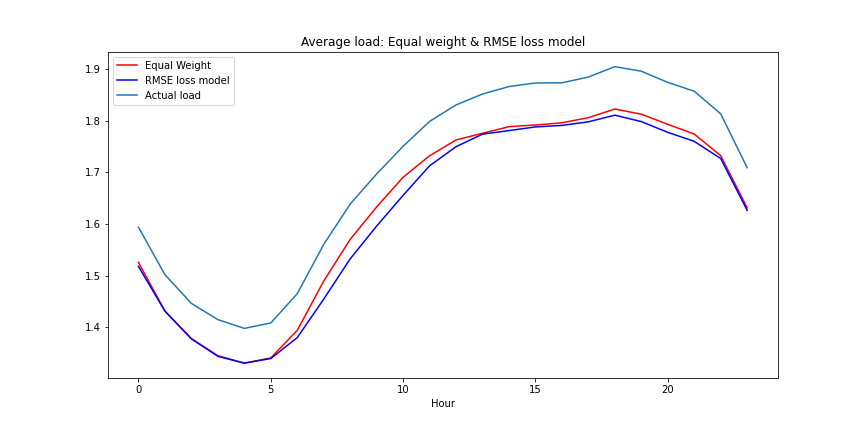
Equal Weights
I first tried training the model in the case that the weights for overgenerating and undergenerating were exactly the same. Not surprisingly, the learned model seems to be very similar to the original RMSE loss model.
Mathematically, the loss function for the optimization problem would just reduce to a scaled mean square error. So training on this loss function would essentially just be like extending training our neural net on the RMSE model for more epochs.
Weight overgeneration by hour to simulate grid cleanliness
Like the metastudy suggested, I then wanted to see how this methodology could be used to schedule electricity generation to reduce GHG emissions.
Grid cleanliness differs by the hour depending on the generation mix. For example, CAISO (the independent system operator my region is under) has grid emissions differing by hour like shown below. There are less emissions during the day when the sun is out and higher otherwise. Grid emissions differ also by the time of year, but we can use the hourly average to start with.
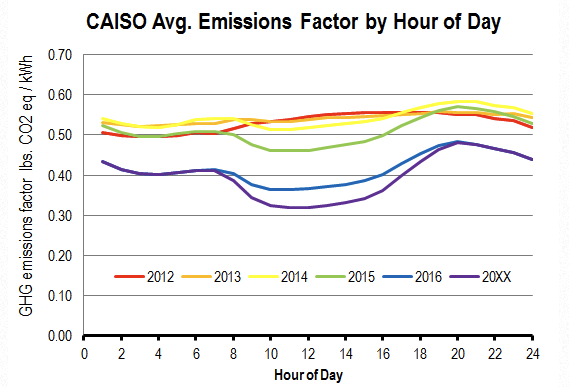
We can try to minimize the GHG emissions by considering emitting GHGs as an overgeneration cost. Additionally, we can modify our optimization problem to have differing weights for overgeneration by the hour to capture the differing GHG emissions by time of day.
As an estimate, I used overgeneration and undergeneration weights in the graph below. For undergeneration, I used a constant weight of 25 while for overgeneration, I used the values for ‘20XX’ in the Beyond Efficiency blog above and scaled it to have an average value of 25.
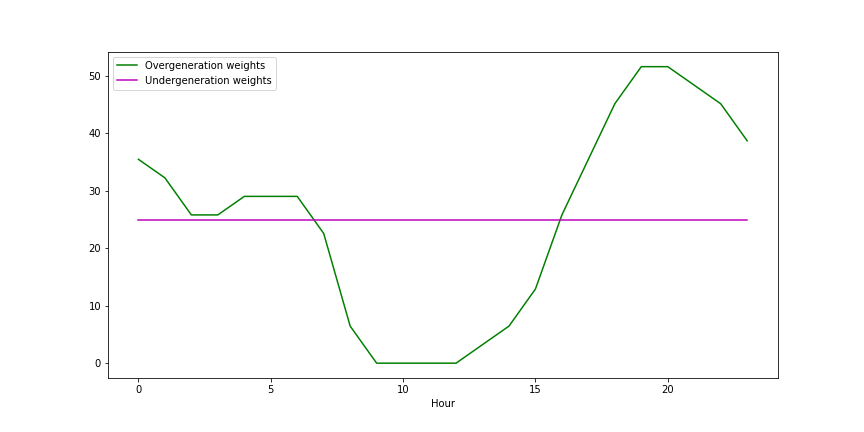
Using these weights, I then trained the neural network according to this new task loss which includes costs of both undergenerating and overgenerating during high emission times. I compare this new model (Task loss including emissions) with the RMSE loss model below.
We can see that it is now balancing the costs of undergenerating with the grid emissions, overgerating during day time hours and undergenerating during “dirtier” hours in the early morning and evening hours!
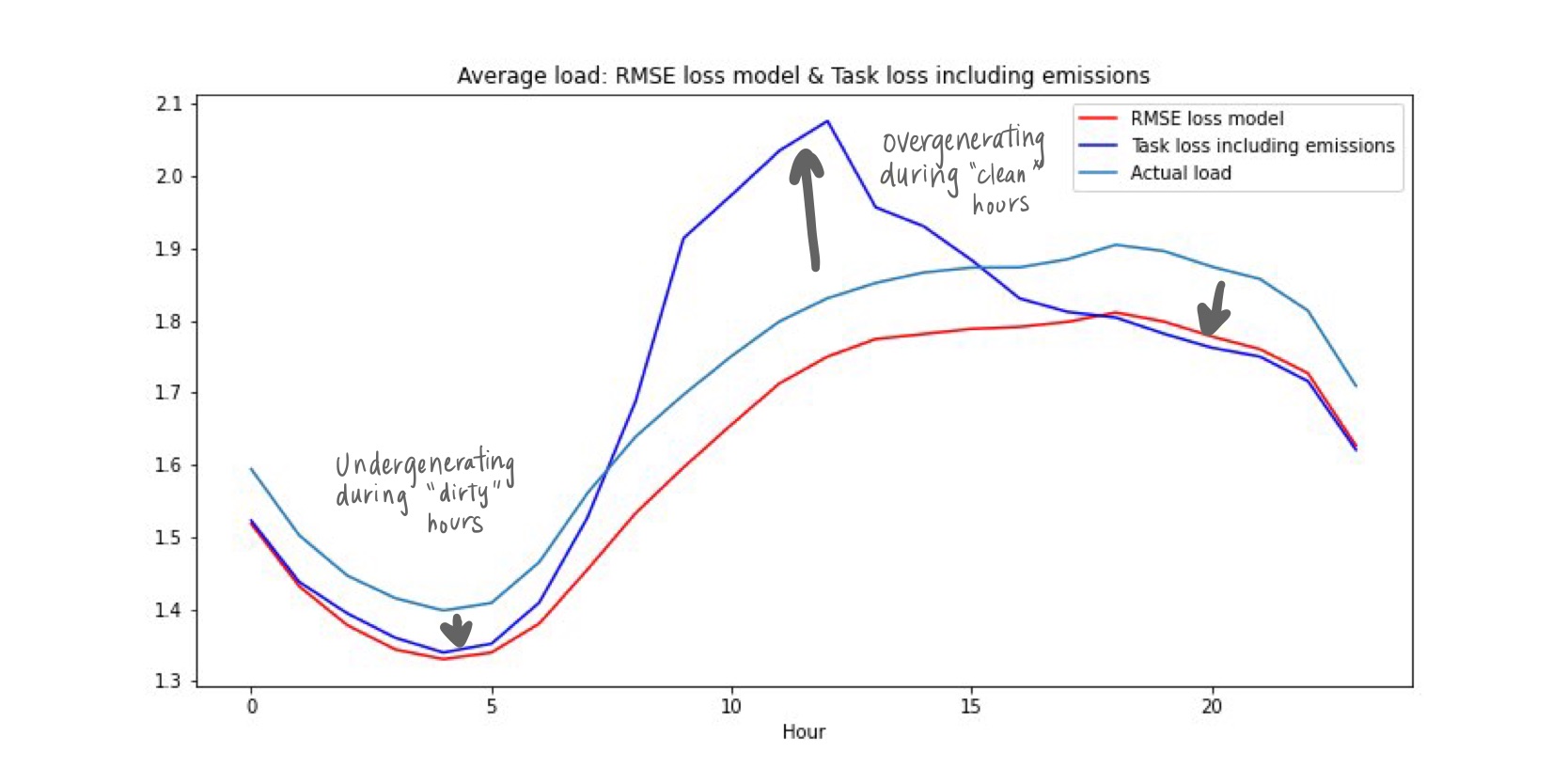
It’s worth noting that there needs to be some tuning of the weight sizes to achieve the effect desired and there might need to be some tinkering to figure out how the weight sizes affect the magnitude of change in the model.
Takeaways
This was a pretty fun project showing how models could be tuned to optimize for certain effects. Especially for applications where there are large ramifications of overpredicting or underpredicting, or more complex situations where there are competing priorities, this definitely seems applicable.
One of the caveats though is that the process of finding the solution to the optimization problem needs to be differentiable so gradient descent may be applied through the optimization process. So, the nature of the optimization problem may need to have some constraints!
Places to Improve
I didn’t focus too much on hyperparameter tuning for this project, but it looks like there are places where that would benefit. For example:
- The initial neural net model may be overlearning to the training data. It would benefit from investigating a dev or test learning curve as well to see if this is the case. In general, I should have probably plotted the training and test learning curves together!
- For the Task loss model, the training learning curves are very noisy. It may be better to use a smaller learning rate or implement learning rate decay. Additionally, there is the convergence of the quadratic program itself. The threshold of convergence may need to be lowered so the model produces better and more consistent estimates to optimization problem solution.
- It takes a much longer time for the optimization training to happen compared to the neural net. There are probably ways I can improve my code to run faster or change my batch sizes.